排序算法集合
排序算法可以说是算法中最基础的,但是一直以来都没有系统地去整理过,而且其中有些细节还是值得好好推敲的,因此把遇到过的排序算法进行整理了一下。目前整理地还不够全面,后续会继续慢慢完善。
1. 冒泡排序
冒泡排序就是通过比较相邻两数大小,以前小后大的的规则,如不满足则交换两者位置,继续比较下一组相邻两数,以此将最大数由前慢慢移动到后面的一种排序算法,由于大的数是一点点移动到最后面的,所以称为冒泡排序。
可以用以下场景来理解:在一队乱序排列的人中,只有左边的人知道自己比右边的人高或者低,由左边的人决定两人是否交换位置,然后从左到右进行比较,此时可以得出此队最高的人会站在最右边。之后用此方法选出次高,第三高…的人,即可完成队列的由低到高的排序。下列图片只做了一次比较,后续循环太多就不展示了。

func BubbleSort(s []int) []int {
for i := 0; i < len(s)-1; i++ {
for j := 0; j < len(s)-i-1; j++ {
if s[j] > s[j+1] {
s[j], s[j+1] = s[j+1], s[j]
}
}
}
return s
}
2. 选择排序
选择排序是在数组范围内先找出最小的数,放置在第一个位置,再从剩下数中找出最小的数,放在第二个位置,以此类推,直到最后一个数放置在数组的最后一个位置。

func SelectionSort(s []int) []int {
for i := 0; i < len(s)-1; i++ {
minIdx := i
for j := i + 1; j < len(s); j++ {
if s[minIdx] > s[j] {
minIdx = j
}
}
if i != minIdx {
s[i], s[minIdx] = s[minIdx], s[i]
}
}
return s
}
3. 插入排序
插入排序类似于我们打扑克,将数组分为两部分,左半部分是已排序数列,右半部分是未排序的,从未排序的数列中取出第一个数,依次与其左边的数进行比较,当比左边的数小时,将其左边的数向右移动一位,直到比左边数大的时候,将其插入。

func InsertionSort(s []int) []int {
var left int
for i := 1; i < len(s); i++ {
left = i - 1
current := s[i]
for left >= 0 && current < s[left] {
s[left+1] = s[left]
left--
}
s[left+1] = current
}
return s
}
4. 归并排序
归并排序的核心思想是是将两个已经排好序的数组进行合并,以达到最终有序的状态。如何得到两个排好序的数组就是需要将数组进行拆分,从单个元素开始合并,得到多个有序的长度为2的数组,然后再继续合并得到多个有序的长度为4的数组,主要通过递归的方式进行处理,将数组逐级折半拆解,直到元素为一个进行合并处理。

// l一般为0,表示s的起始元素下标,r表示slice s的最后一个元素下标
func MergeSort(s []int, l int, r int) []int {
// 说明此时只有一个元素,达到有序状态了
if l >= r {
return s
}
m := (l + r) / 2 // 折半拆解
MergeSort(s, l, m)
MergeSort(s, m+1, r)
return merge(s, l, m, r) // 合并拆解的流程
}
// 对已排序数组进行合并排序
func merge(s []int, l, m, r int) []int {
ls := make([]int, m-l+1)
rs := make([]int, r-m)
copy(ls, s[l:m+1])
copy(rs, s[m+1:r+1])
lsIdx, rsIdx, sIdx := 0, 0, l
// 两数组均未排序完
for lsIdx < len(ls) && rsIdx < len(rs) {
if ls[lsIdx] < rs[rsIdx] {
s[sIdx] = ls[lsIdx]
lsIdx++
} else {
s[sIdx] = rs[rsIdx]
rsIdx++
}
sIdx++
}
// rs数组排序完,只需将ls数组补充到后面即可
for lsIdx < len(ls) {
s[sIdx] = ls[lsIdx]
lsIdx++
sIdx++
}
// ls数组排序完,只需将rs数组元素补充到数组后面
for rsIdx < len(rs) {
s[sIdx] = rs[rsIdx]
rsIdx++
sIdx++
}
return s
}
5.快速排序
快速排序是依据数组中的一个元素,将数组划分为两部分,比ta他小的在左边,比它大的在右边,然后通过分治的方式,不断缩减划分范围,以得到最终有序的数组。
快速排序的核心就是对数组进行划分,主要维护两个指针,一个指针遍历未排序数组,一个指针作为与对比数大小的分界线。
第一步:原始数组为[3, 5, 2, 4, 1] 以最后一个元素 1 为比较对象,发现前面没有一个比 1小的数字,分界指针未移动,一致在第一个位置,所以最后互调分界指针和 1 的位置
第二步:将数组进行拆分,元素 1 之前的为一部分, 之后的为一部分,对剩余的 [5, 2, 4, 3],继续进行划分,以最后一个元素 3 作为分界依据,第一个元素 5 比 3 大,分界指针不移动,第二个元素 2 比 3 小,需要将第二个元素与分界元素进行互换,即 2 5 交换,然后分界指针向前移动,后续的 4 也比三大,不需要处理,最终得到的顺序是 [2 ,3, 4, 5]
第三步:继续划分,按照3的位置划分为两部分,一部分是 [2] 另一部分是 [4, 5], 重复第二步,
第四步:所有拆分到最细粒度的数组都不需要再拆分了,则数组达到有序状态。

// QuickSort 快速排序
func QuickSort(s []int, l, r int) []int {
if l >= r {
return s
}
sep := partition(s, l, r)
s = QuickSort(s, l, sep-1)
s = QuickSort(s, sep+1, r)
return s
}
// 将区间s[l,r]进行划分
func partition(s []int, l, r int) int {
// 作为划分的界限判断值
sep := s[r]
// 划分界限的索引
sepIdx := l
for i := l; i < r; i++ {
if s[i] < sep {
s[sepIdx], s[i] = s[i], s[sepIdx]
sepIdx++
}
}
s[sepIdx], s[r] = s[r], s[sepIdx]
return sepIdx
}
6. 堆排序
堆排序是以通过维护最大堆和最小堆的方式,对数组进行排序的一种算法。
最大堆:父节点比子节点都要大的堆
最小堆:父节点比子节点都要小的堆
堆:可以近似理解为完全二叉树
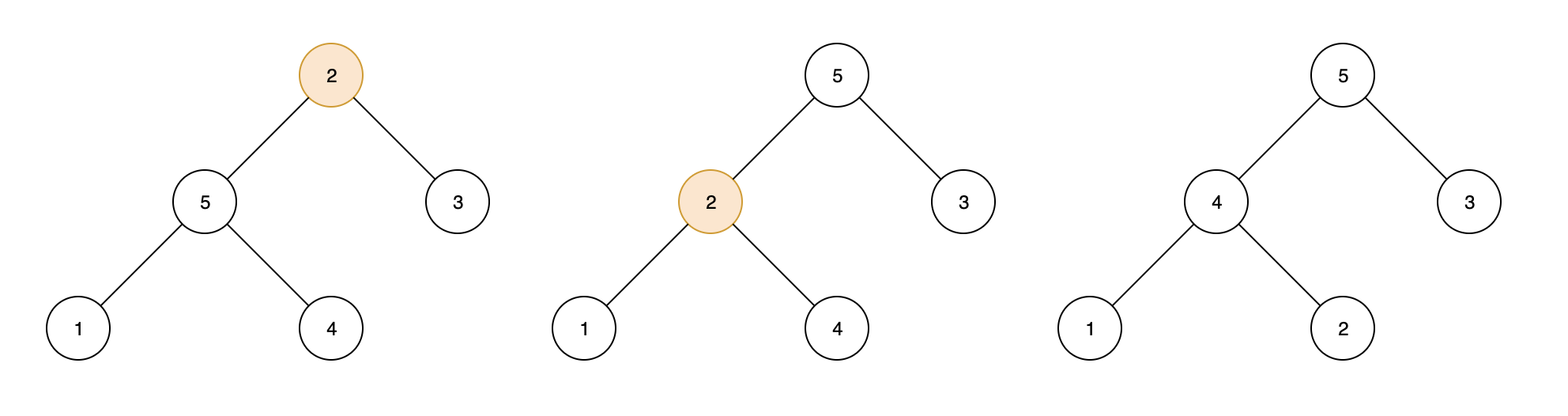
最大堆的维护:这是堆排序的算法核心,是为了确保当前节点的数值比子节点的数值要大。主要由函数 maxHeapify 维护,其主要算法逻辑如下:寻找当前节点和其子节点中最大的数,将其与当前节点交换,并继续确保被交换的节点仍然满足最大堆规则。
如下图所示,对于根节点 2 而言,它不是所有节点中的最大值,所以不满足最大堆的规则,在它和它的子节点中找到最大值,设置为父节点,得到图二;但是此时2号这个节点依旧不满足最大堆规则,继续上述流程,将 2 与 4进行交换,最终得到一个最大堆。
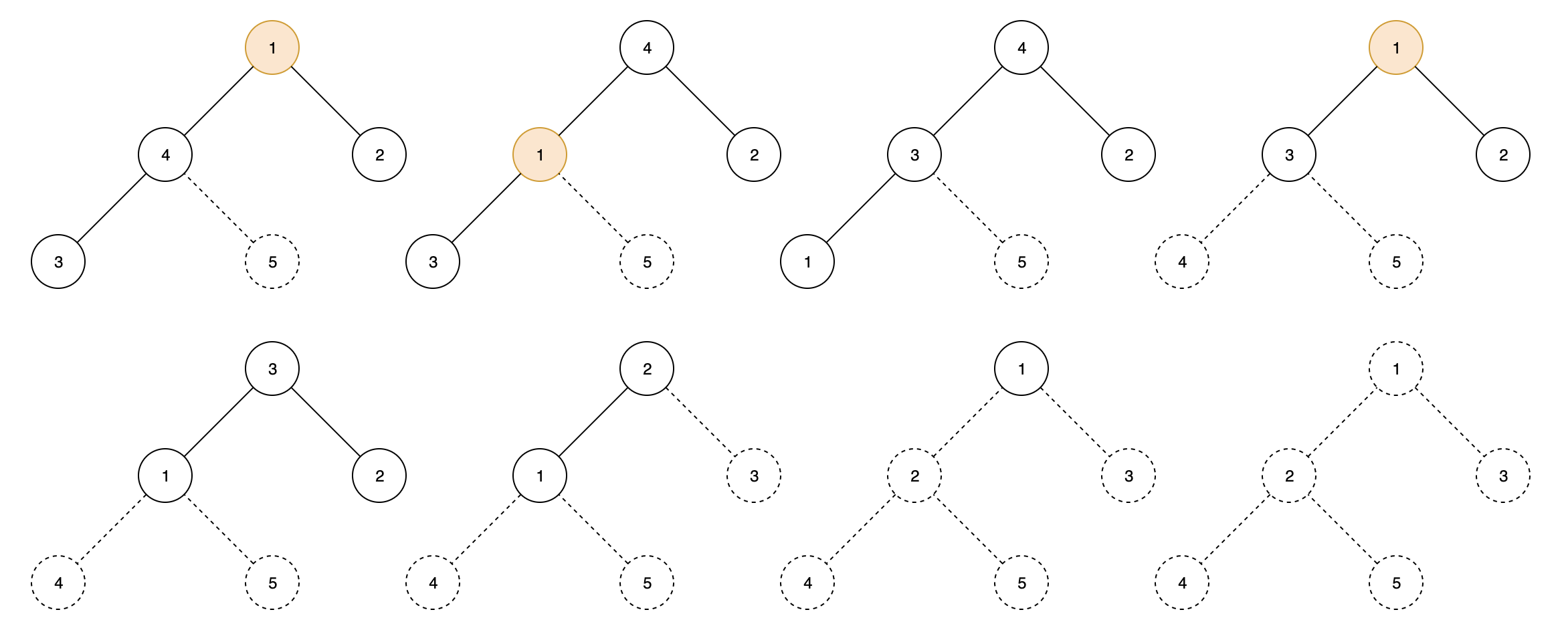
最大堆构建:有了最大堆的维护逻辑,我们就可以将数组转化为一个最大堆了,只需要从叶子节点的父节点开始,慢慢到根节点,不断地进行最大堆的维护即可得到一个最大堆。

堆排序:堆排序就是将最大堆堆顶元素与最后一个元素进行交换,继续维护从堆顶到倒数第二个元素间的最大堆操作。由此将每次得到的最大堆的堆顶元素提取出来,即可得到有序列表了。
// HeapSort 堆排序
func HeapSort(s []int) []int {
buildMaxHeap(s)
heapSize := len(s)
for i := len(s) - 1; i >= 0; i-- {
// 第一个节点为未排序列表最大数,防止在未排序数组最后一个位置
s[i], s[0] = s[0], s[i]
// 此时堆的大小需要减1,防止在维护最大堆的时候,将已排好序的数据打乱
heapSize--
// 每次都从根节点开始重新维护一个最大堆
maxHeapify(s, heapSize, 0)
}
return s
}
// 最大堆的构建:实则为从叶子节点的父节点开始不断维护最大堆,直到根节点,完成最大堆的构建
func buildMaxHeap(s []int) {
for i := len(s)/2 - 1; i >= 0; i-- {
maxHeapify(s, len(s), i)
}
}
// 最大堆的维护,以确保父节点比子节点都要大
// 前提:只有 i 节点不满足最大堆的要求,其余节点都满足
func maxHeapify(s []int, heapSize, i int) {
l := left(i)
r := right(i)
largestIdx := i
// 寻找父子节点中的最大值
if l < heapSize && s[l] > s[largestIdx] {
largestIdx = l
}
if r < heapSize && s[r] > s[largestIdx] {
largestIdx = r
}
if largestIdx != i {
s[i], s[largestIdx] = s[largestIdx], s[i]
// 因为当前节点变更,后续不一定满足最大堆,需要继续判断处理
maxHeapify(s, heapSize, largestIdx)
}
}
// 根节点从0开始,左子节点索引:2 * i + 1
func left(i int) int {
return 2*i + 1
}
// 根节点从0开始,右子节点索引:2 * (i + 1)
func right(i int) int {
return 2 * (i + 1)
}
7. 计数排序
计数排序就是对于一个元素均为 0~k 之间的数组,采用一个长度为 k 的数组,以原数组数值作为计数数组的索引下标,记录排序数组中每个元素的出现次数,再依据出现次数,对此数组次数进行位置索引,最后将原数组按照计数数组中的索引进行重新排序的一种排序算法。
具体流程如下:
- 原数组 [3, 5, 2, 4, 1, 3]
- 计数数组按照原数组的值作为索引,得到[0, 1, 1, 2, 1, 1],其中2表示数字3在原数组中出现2次。
- 对计数数组中的次数累加作为元素的索引得到[0, 1, 2, 4, 5, 6]其中 4 表示数字3在排序后数组中的第 4 个位置,且当第一个 3 放置在数组中之后,需要减一,以便将第二个 3 放置在数组中第 3 个位置。

// CountingSort 计数排序
func CountingSort(s []int, k int) []int {
c := make([]int, k) // 存储每个数出现的次数
for i := range s {
c[s[i]] = c[s[i]] + 1 // 出现次数+1
}
//整理每个数出现的顺序
for i := 1; i < k; i++ {
c[i] = c[i] + c[i-1]
}
b := make([]int, len(s))
for i := range s {
b[c[s[i]]-1] = s[i] // 索引从0开始
c[s[i]]--
}
return b
}
8. 桶排序
桶排序是通过将数组中的元素按照区间进行划分,放置在不同的桶中,然后再针对每个桶中的元素使用其他排序算法进行排序,最后将所有桶中的元素依次取出的一种排序算法。
如下图:将原数组分为两个桶,[3, 2, 1] 和 [5, 4] 在分别对两个桶中的元素进行快速排序,得到[1, 2, 3] 和 [4, 5] 最后将每个桶中的元素组合起来得到排序好的数组 [1, 2, 3, 4, 5]

// BucketSort 桶排序
func BucketSort(s []int, bucketsNum int) []int {
buckets := make([][]int, bucketsNum)
// 获取数组中的最大值和最小值,以确定如何桶的区间大小
max, min := math.MinInt32, math.MaxInt32
for _, v := range s {
if max < v {
max = v
}
if min > v {
min = v
}
}
// 将不同的数按照桶的区间落在不同的桶中
for _, v := range s {
id := getBucketID(min, max, bucketsNum, v)
if len(buckets[id]) == 0 {
buckets[id] = []int{v}
} else {
buckets[id] = append(buckets[id], v)
}
}
// 桶的编号由小到大,其中的数据也是由小到大
ret := []int{}
for _, bucketList := range buckets {
// 针对每个桶中的数据进行快速排序
ret = append(ret, QuickSort(bucketList, 0, len(bucketList)-1)...)
}
return ret
}
// 判断一个数落在哪个桶中
func getBucketID(min, max, num, key int) int {
step := (max-min)/num + 1
return (key - min) / step
}
参考资料
- 算法导论
- 维基百科
